D-Star-Light: Searching in Dynamic Space

Prerequisites

If you are not familiar with A* search, here is a great article to get started. D-Star-Lite and this article is based on A* search.
D-Star-Lite was proposed by 的Sven Koenig and Maxim Likhachev from Georgia Institute of Technology. This is the original thesis: http://idm-lab.org/bib/abstracts/papers/aaai02b.pdf

Why D-Star-Lite?

Searching Algorithms are the cores of navigation systems and motion planning. You are probably familiar with searching algorithms like Breadth-First Search, Depth-First Search, or the more advanced A* search.

In reality, environment are constantly changing. These algorithms assume the environment to be static. To deal with it, we can simply do re-searching whenever the environment changed. But this kind of approach may suffer from inefficiency, even a small change of the world would introduce the re-computation of every single step.

Is there a way to update only the necessary steps? The following example shows that we only need to compute the green part of the path instead of the old path.

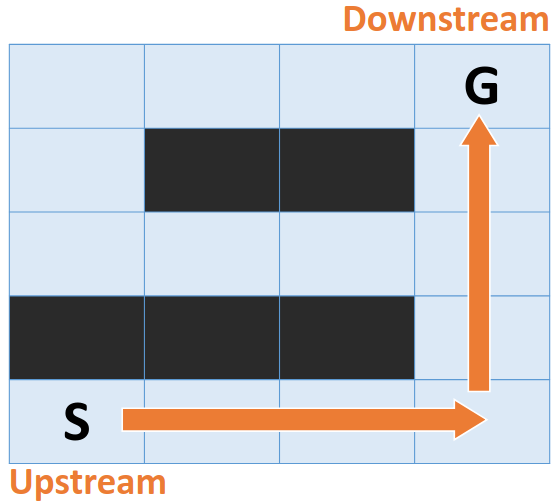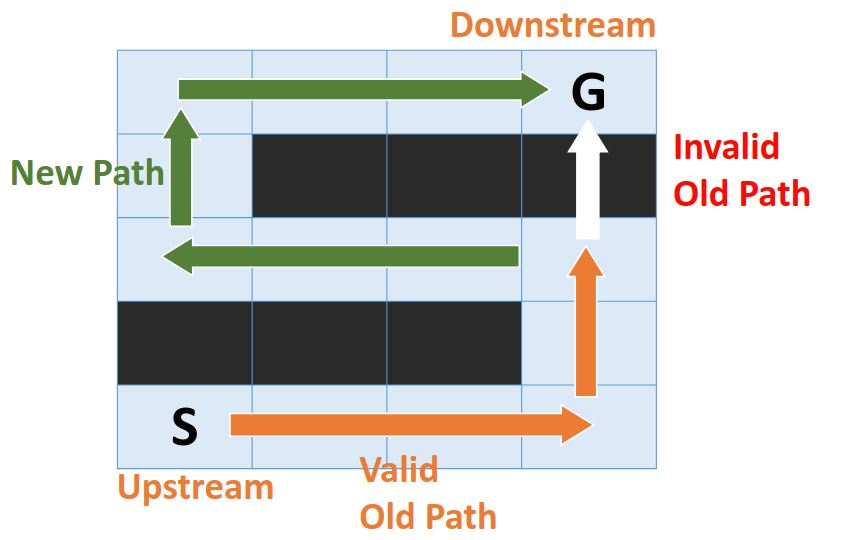Here comes the D-Star-Light, the Dynamic version of A. It works similar to A, but computes only the necessary nodes to update the shortest path when environment is changed.

Min-Queue and DP Propagation

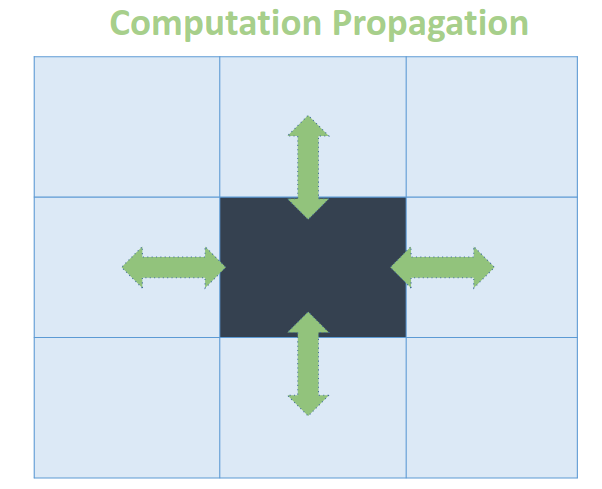
Before we get started, let’s visualize the how A* works:

a-star

As you can see, the computation propagates from the starting node to the destination mode. More precisely, the computation propagates from nodes with smaller cost to nodes with bigger cost. This is the result of the min-queue and the DP fashioned cost propagation formula. The min queue ensure that the current smaller nodes always get computed earlier then bigger nodes. The DP formula propagates the computation from nodes to nodes.

Here are the two important properties that hold both in A* and D*-Lite:

Min Queue:

In the min-queue, the node with minimal cost pops and gets visited earlier. This property ensures the computation on each node goes in an ascending order.

DP Propagation Formula

$g(s) = \begin{cases} 0 & \text{if s is start point} \\ min_{s' \in Preds(s)} (c(s, s') + g(s')) & \text{otherwise,} \end{cases}$

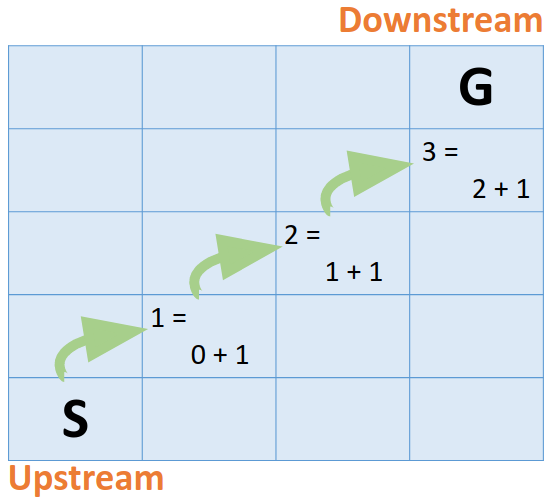
The computation of a node depends on it’s predecessor with the minimal cost. In the other hand, if the cost of the node is the minimum to the successors, it propagates the computation to the successors. This property results the “Upstream” and the “Downstream”. Upstream nodes propagates the computation to the downstream nodes.

D-Star-Lite:

But how do we apply this two ideas in dynamic environments? It’s simple. When change happens, we propagate the update to it’s neighboring nodes. The neighboring nodes then propagate further to their neighboring nodes, resulting a computational ripple. The DP formula decides how to propagate the update while the min-queue decides the order of the propagation.

To implement this ideas, D-Star-Lite introduces two values to stores the cost of each node, g(s) and rhs(s). g(s) is pretty similar to the g(s) in A. The difference is that *g(s) in d-star-lite is the “historical value” of the cost. In dynamic environments, we need to memorize the cost of each node since the last change.

The rhs(s) value stands for right-hand-side value. The value of rhs(s) and g(s) will be equal eventually. But the role of rhs(s) is to obtain the latest update. The information of rhs(s) is alway newer or at least as new as g(s).

$rhs(s) = \begin{cases} 0 & \text{if s is start point} \\ min_{s' \in Succ(s)} (c(s, s') + g(s')) & \text{otherwise,} \end{cases}$

For a node s, we can determine whether s needs to update when the environments changed.
In a node s:

In a node s:
  If rhs(s) == g(s) ---> Update is complete, the cost of s is ready and reliable.
  If rhs(s) != g(s) ---> Update is needed, insert this node into the min-queue for the update.

Since we have two values describing the cost of a node, min-queue needs a little tweak to compare nodes. The following two keys values, K1 and K2 are introduced for nodes comparison. $key(s) = [k_1(s), k_2(s)]\\ = [\min(g(s), rhs(s)) + h(s),\\ min(g(s), rhs(s)) ]\\$

Node u  > v
  when K1(u) > K1(v) or K1(U) == K1(U), K2(u) > K2(v)

It’s similar to A, the difference is we now comparing the minimum of *[g(s), rhs(s)]. As for *K2, it’s just K1 subtracts the heuristic value h(s). K2 serves for extra comparison when K1 are equal.

Pseudo code

In main function. the critical parts are ComputerShortestPath() and UpdateVertex(u). ComputerShortestPath() returns the shortest path and UpdateVertex() deals with the change of the world.

main():
  Initialize()
  Forever:
    ComputerShortestPath() #pop each s from min-queue and making g(s) = rhs(s)
      if change happens:
        for all directed edges(u, v) with cost changed:
          update the edge cost c(u, v)
          UpdateVertex(u) #Update the rhs(u) and put it into min-queue

In initialization, assign everything infinity, except rhs(s_start). This makes D-Star-Lite begins to explore from the starting point.

Initalize（）:
  for all nodes s in graph:
    g(s) = rhs(s) = INF
  rhs(s_start) = 0
  min_queue.insert(s_start)

To compute the shortest path, we keep popping the queue and computing the cost until we get a reliable cost of the starting point (g(s_start) == rhs(s_start)). There are two different the cost of node s.

If g(s) > rhs(s), we simple assign rhs(s) to g(s), meaning this node is reliable and updated. Since node s is updated and has new cost, we need to update the child nodes of s.

In the case of g(s) < rhs(s), we assign Infinity to g(s) and update s and it’s child nodes.
Why don’t we just assign rhs(s) to g(s) just like the previous case?
The reason is that g(s) is the historical cost. Even though g(s) is the minimum of the queue, it’s not reliable because node s might have some “Upstream” waiting in the min-queue. By calling UpdateVertex(s), we make sure we can compute the upstream of s before “converging” node s.

ComputerShortestPath():
  While min_queue.min() < s_start or g(s_star) != rhs(s_start):  #Keep compute until we find a reliable cost of s_start
    u = min_queue.pop() #Get the minimum of the queue
    if(g(u) > rhs(u)):  #Converge u in this case
      g(u) = rhs(u)
      for all u' in successors of u"
        UpdateVertex(u')
    elif(g(u) < rhs(u)): #node u needs to update the value again.
      g(u) = inf
      UpdateVertex(u')
      for all u' in successors of u"
        UpdateVertex(u')

  min_queue.remove(u) if u in min_queue
  min_queue.insert(u) if g(u) != rhs(u)

To update the change, we only need to update the rhs value and insert the node into queue when g(u) != rhs(u)

UpdateVertex(u):
  rhs(u) = g(u') + c(u', u) where u' has the minimal rhs among predecessor of u
  min_queue.remove(u) if u in min_queue
  min_queue.insert(u) if g(u) != rhs(u)

Let’s visualize how D-Star-Lite propagate the computation:

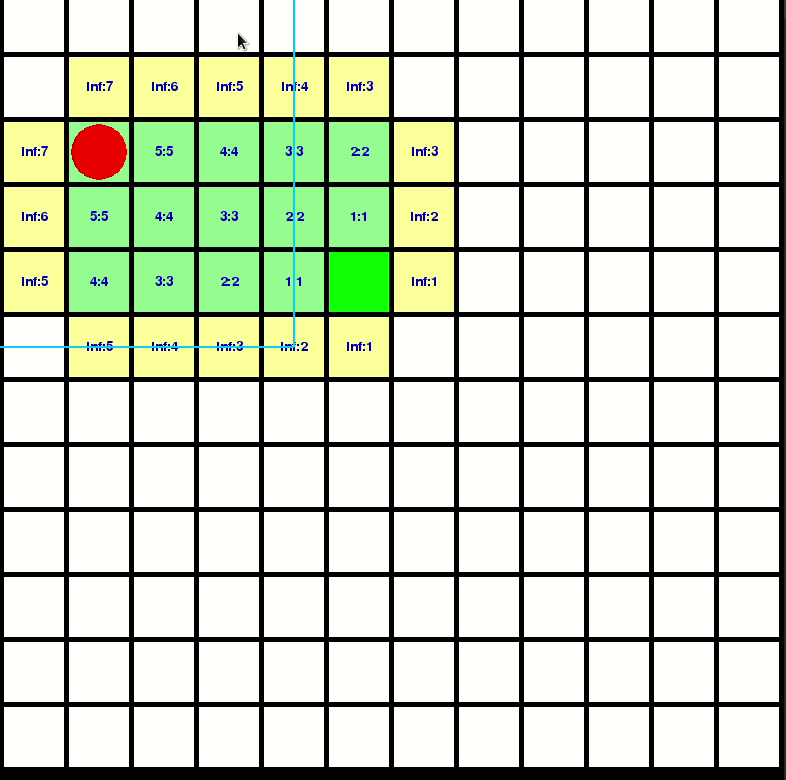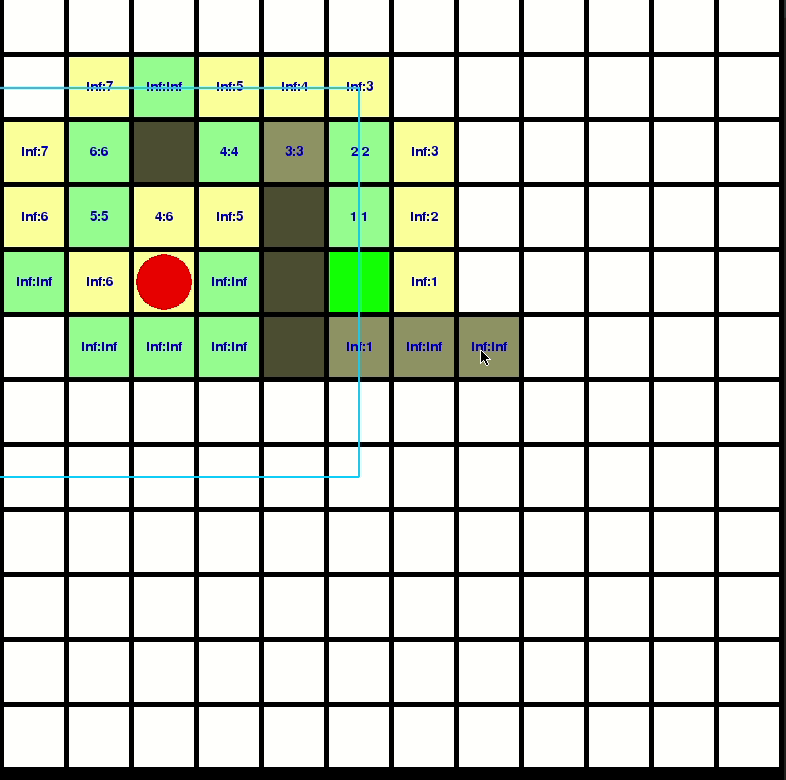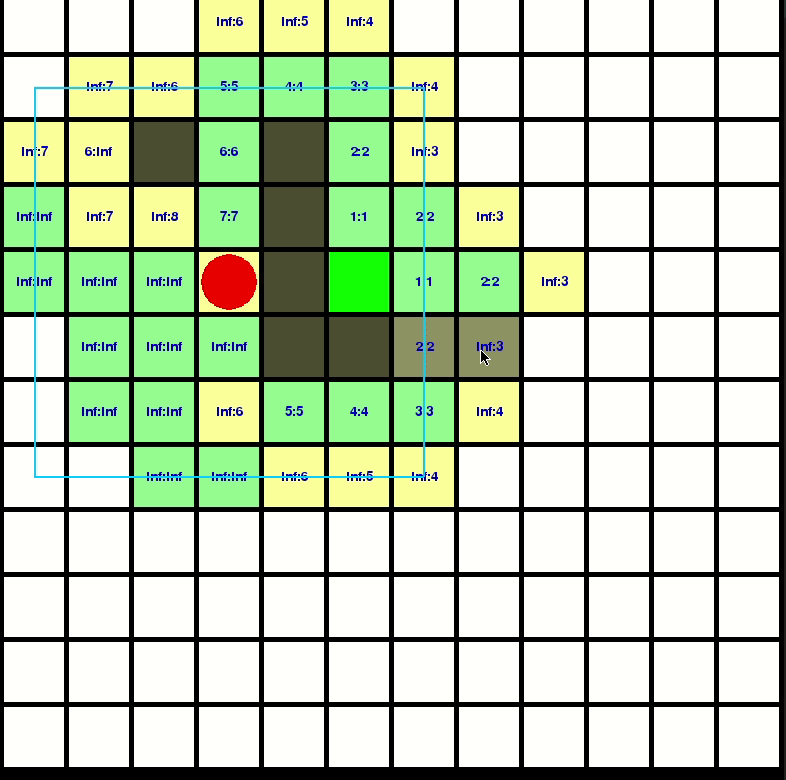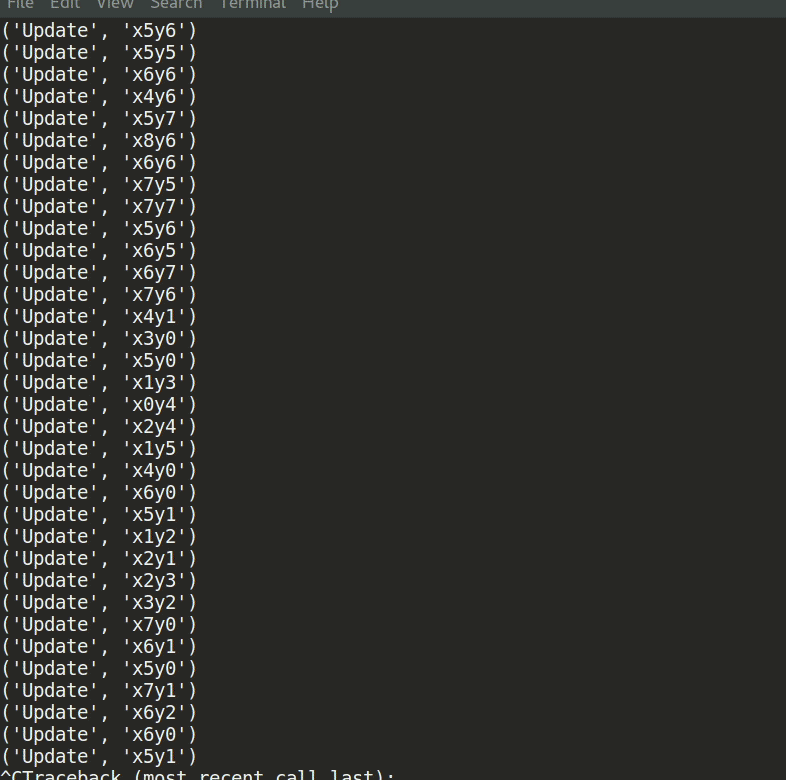
You can check my repo for better understanding: https://github.com/GBJim/d-star-lite