D-Star-Light: 動態環境中的搜尋法

必要知識

如果你不熟悉 A search的話, 可以參考這篇文章(http://theory.stanford.edu/~amitp/GameProgramming/AStarComparison.html) D-Star-Lite演算法和這篇文章都是以A*為基礎做延伸的
D-Star-Lite由Georgia Institute of Technology的Sven Koenig 及 Maxim Likhachev提出, 有興趣可以閱讀原文

D-Star-Lite可以幹麻呢?

搜尋演算法相當重要, 常見的導航系統以及自駕車輛的路徑規劃, 都需要一個搜尋演算法作為核心, 你可能熟悉BFS或是DFS這類的搜尋法, 或是更有效率的A*搜尋

但些算法所假設的環境是靜態的, 無法處理真實世界中的動態環境. 雖然我們可以用簡單暴力的方式做重新搜尋: 只要環境一變動, 立即重新搜尋
但這種方式有非常高的cost, 任何風吹草動都會導致我們要重新搜尋一遍

當環境變化時, 如果我們只更新必要的部份, 而不是計算全部的路徑, 便能省下大量的成本

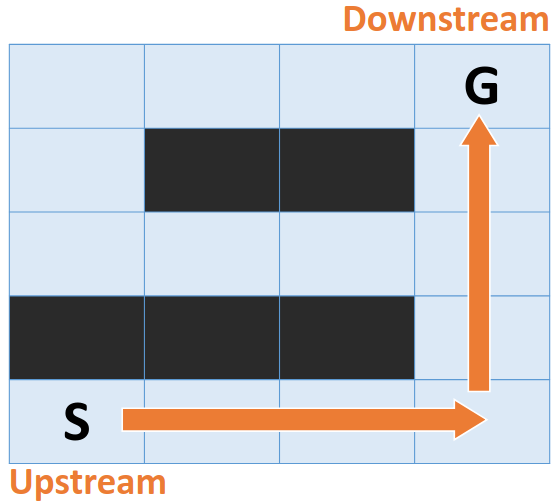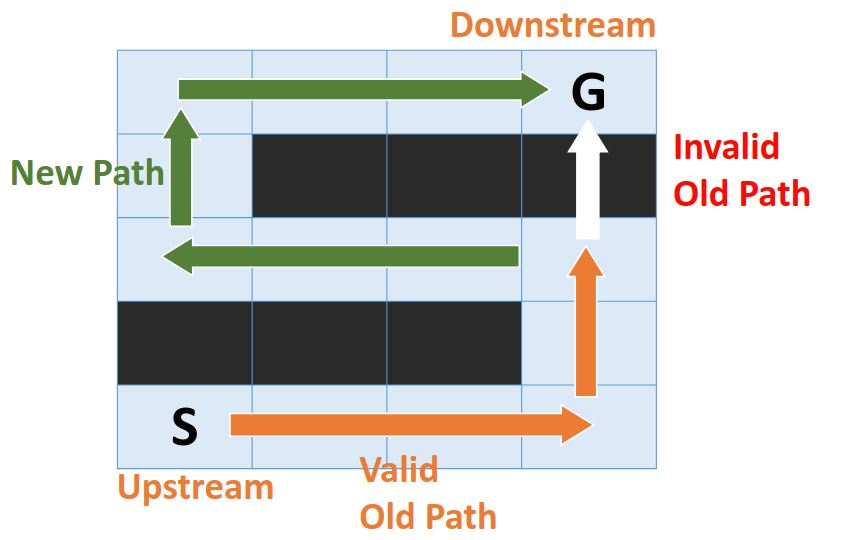此時我們就需要D-Star-Lite, Dynamic版本的A*. 它是A*的擴展
當環境發生變化的時候, 它能更新必要的路徑, 有效率的計算新的cost

Min-Queue 與 DP傳播

開始介紹算法觀念之前, 我們先看看A*算法的視覺化

a-star

你可以看到, 計算由起點擴散到終點, 更準確的來說, 計算是由cost低的節點往cost高的節點擴散的. 這個是 min-queue和DP擴散所導致的
min-queue確保cost小的node可以比cost高的node更優先計算, 而DP(Dynamic Programming)擴散意味著cost是在node中相互傳遞

這兩個便是A*以及D-Star-Lite的核心概念

Min Queue:

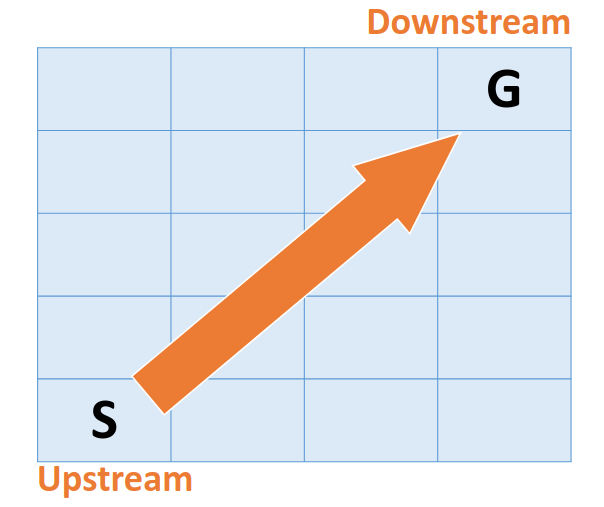
在Min-quque中, 有當前最小值的節點總是優先被選中, 導致計算總是由最小的節點開始, 一步步往cost高的節點移動

DP 傳播公式

$g(s) = \begin{cases} 0 & \text{if s is start point} \\ min_{s' \in Preds(s)} (c(s, s') + g(s')) & \text{otherwise,} \end{cases}$

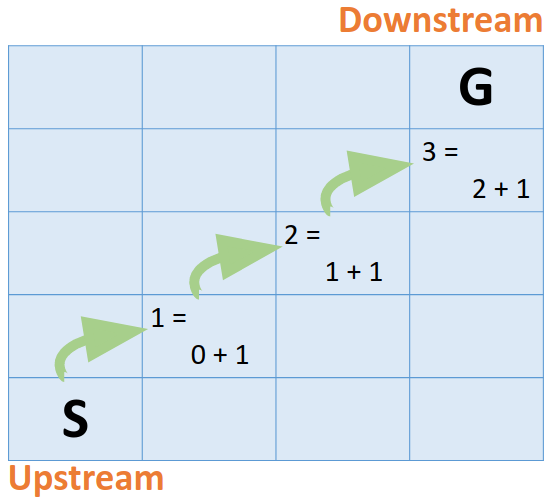
從這個式子可以看出, 一個節點的cost的計算依賴於它的母節點
另外, 如果這個節點的cost夠小, 它也會傳播給它的子節點
這種傳播導致了節點會有上游以及下游的概念, 上游節點的資訊傳播給下游節點

D-Star-Lite:

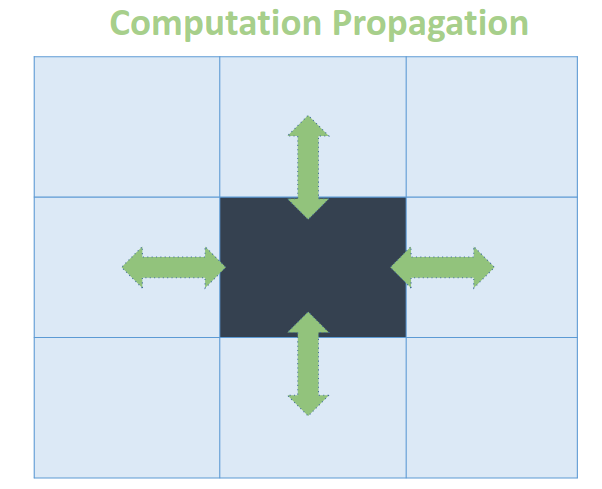
這兩個核心概念如何處理動態環境呢？相當簡單, 當環境發生變動, 我們便更新對應的節點, 這個被更新的節點便擴散到他的鄰近節點, 鄰近節點再擴散它的周圍,形成一種計算漣漪
DP傳播定義了cost如何擴散, 而Min-queue則決定了擴散的順序

D-Star-Lite引進了兩個數值來實現這個像法, g(s)以及rhs(s)
g(s) 與A*中的g(s)類似, 差別在於這個g值代表著節點s的歷史值
在動態環境中, 我們需要一個機制去記憶cost的變化

至於rhs(s),意思是 right-hand-side value, 它的數值最終會和g(s)相等, 但它的角色是去取得節點s最即時的更新, rhs(s)總是可以拿到比g(s)更新的資訊

$rhs(s) = \begin{cases} 0 & \text{if s is start point} \\ min_{s' \in Succ(s)} (c(s, s') + g(s')) & \text{otherwise,} \end{cases}$

當環境變動的時候, 我們可以利用,rhs(s)以及g(s), 來決定是否要更新節點s,

In a node s:
  If rhs(s) == g(s) ---> 更新完畢, s的cost已經計算完成
  If rhs(s) != g(s) ---> 需要更新, cost已經過時了,把s扔進min-queue之中等待更新,

由於我們引進了兩個值的關係, min-quque需要一種新的比大小方法, 我們用兩種key value, K1和K2來處理大小的比較

$key(s) = [k_1(s), k_2(s)]\\ = [\min(g(s), rhs(s)) + h(s),\\ min(g(s), rhs(s)) ]\\$

Node u  > v
  when K1(u) > K1(v) or K1(U) == K1(U), K2(u) > K2(v)

與A*相當類似, 差別在於我們現在比較g(s), rhs(s)兩者中的最小值. 另外K1和K2的差別只在於是否引進了heuristic value h(s). 當兩個K1相等的時候, 我們便可以用K2來進行額外的比較

來看看Pseudo code吧

Main function中最關鍵的是 ComputerShortestPath() 以及 UpdateVertex(u).
ComputerShortestPath()計算出起點到終點的最小路徑
UpdateVertex() 負責更新環境的變動

main():
  Initialize()
  Forever:
    ComputerShortestPath() #pop each s from min-queue and making g(s) = rhs(s)
      if change happens:
        for all directed edges(u, v) with cost changed:
          update the edge cost c(u, v)
          UpdateVertex(u) #Update the rhs(u) and put it into min-queue

在初始化的過程中, 將所有cost assign為無限大, 除了起點的rhs rhs(s_start) assign成0
這會導致起點的g值與rhs值不一致, 讓演算法開始由起點開始擴散

Initalize（）:
  for all nodes s in graph:
    g(s) = rhs(s) = INF
  rhs(s_start) = 0
  min_queue.insert(s_start)

在最小路徑的計算中, 我們從min-queue中不斷pop出最小的node, 並計算這個node的cost, 這個while迴圈會不斷執行, 直到我們找到從起到終點的最小路徑, 而且這個數值不能是過時的, 也就是g(s_start) == rhs(s_start)

當 g(s) > rhs(s), 我們將 g(s) assign 為rhs(s), 代表這個節點完成了更新, 另外這個更新傳播給他的子節點

當情況是 g(s) < rhs(s), 我們將 g(s) 設為無限大, 並更新這個節點自身以及他的子節點
為什麼不跟上一個case一樣, 將rhs(s) 的值塞給 g(s) ？因為 g(s) 的角色是歷史值. 即時 g(s) 是queue中的最小值, 它很有可能已經過時了, 他的上游可能還在queue中等著呢, 我們利用把它塞回queue的方式, 讓它能夠正確的收斂cost

ComputerShortestPath():
  While min_queue.min() < s_start or g(s_star) != rhs(s_start):  #Keep compute until we find a reliable cost of s_start
    u = min_queue.pop() #Get the minimum of the queue
    if(g(u) > rhs(u)):  #Converge u in this case
      g(u) = rhs(u)
      for all u' in successors of u"
        UpdateVertex(u')
    elif(g(u) < rhs(u)): #node u needs to update the value again.
      g(u) = inf
      UpdateVertex(u')
      for all u' in successors of u"
        UpdateVertex(u')

  min_queue.remove(u) if u in min_queue
  min_queue.insert(u) if g(u) != rhs(u)

節點更新非常簡單, 只要更新按照公式更新rhs值,並把情況符合g(u) != rhs(u)的節點塞進queue中即可

UpdateVertex(u):
  rhs(u) = g(u') + c(u', u) where u' has the minimal rhs among predecessor of u
  min_queue.remove(u) if u in min_queue
  min_queue.insert(u) if g(u) != rhs(u)

來看看D-Star-Lite的計算如何擴散的

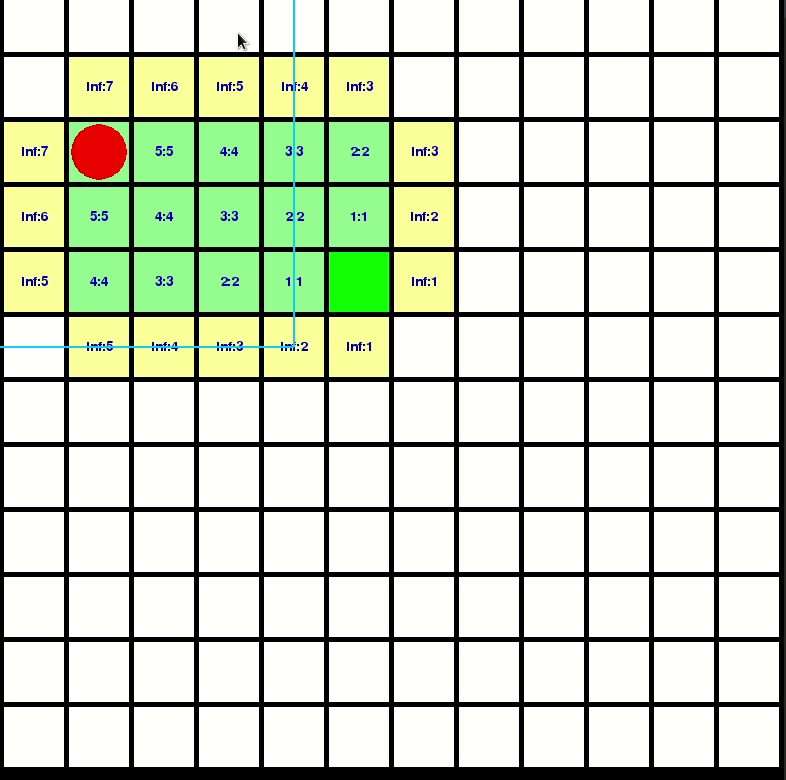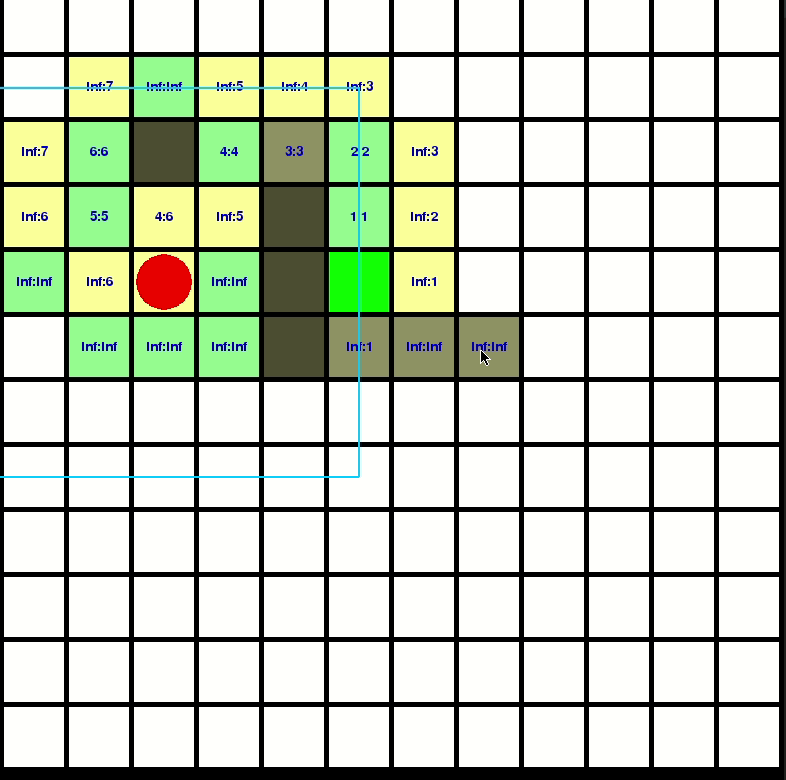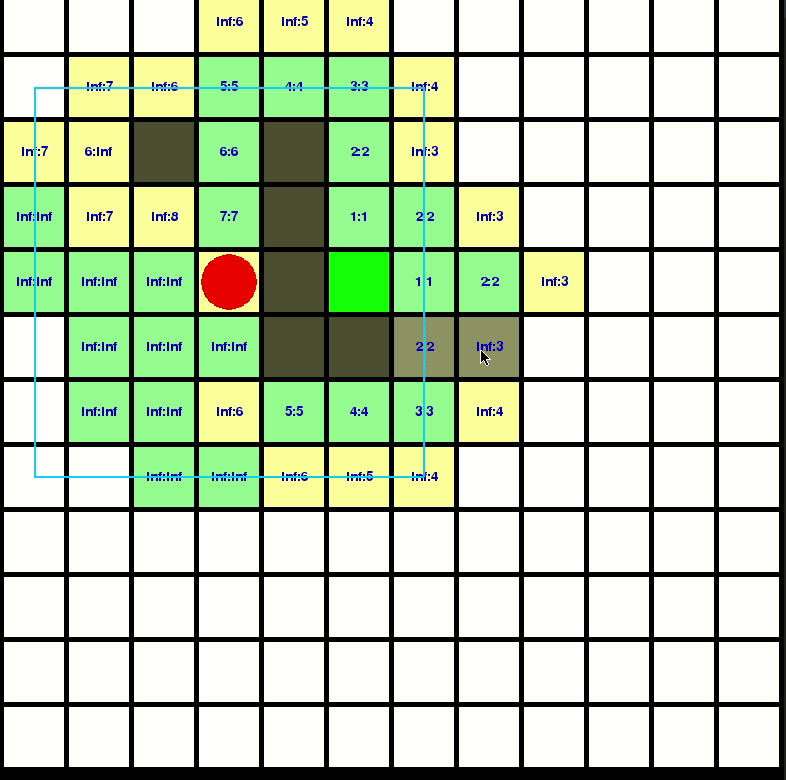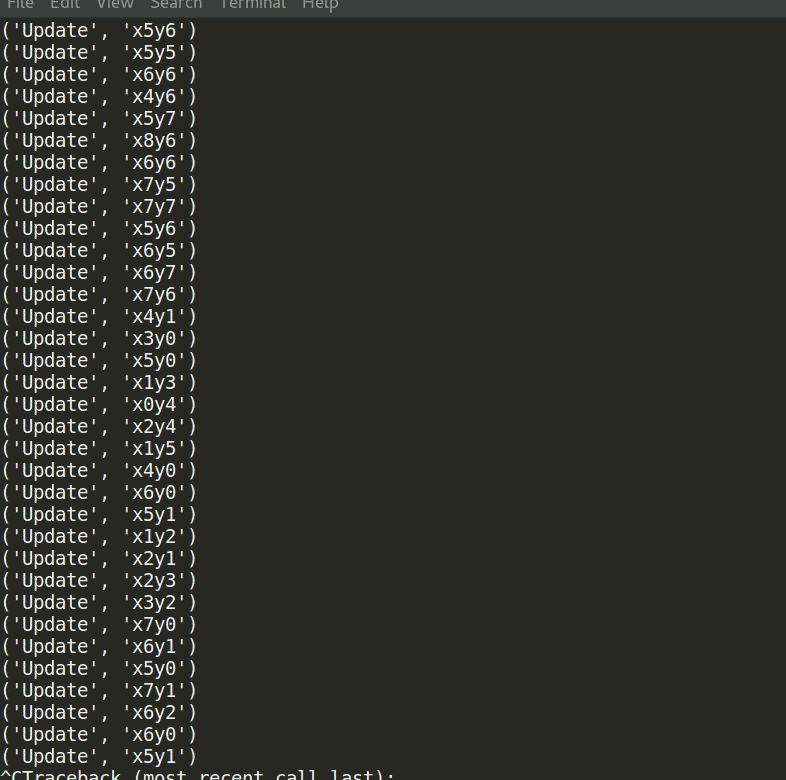
如果想知道實做的更多細節,你可以參考我的repo: https://github.com/GBJim/d-star-lite